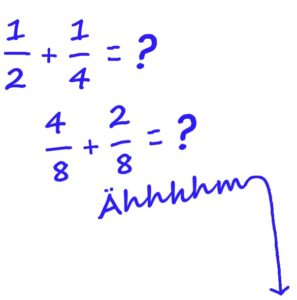Bruchrechnen trieb schon so manchem Elternteil die Schweißperlen auf die Stirn. Wie erklärt man eigentlich, was ein Bruch ist? Wie sieht ein Bruch aus? Welche Brüche gibt es? Zu was braucht man eigentlich Bruchrechnen? Fragen über Fragen, die beantwortet werden wollen!
Montessori-Material hilft dabei, diese Fragen zu beantworten! Es macht Brüche sicht- und greifbar. Außerdem gibt die Hierarchie der Bruch-Übungsmaterialien jederzeit die Möglichkeit, am richtigen Punkt einzusteigen. Beachtet man 2 Kleinigkeiten, wird Bruchrechnen zur neuen Lieblingsaufgabe:
1. Alle Montessori-Materialien bauen aufeinander auf
So natürlich auch das Bruchrechen-Material. Verwendet man diese in der vorgesehenen Reihenfolge, steigern sich die Anforderungen und das Gelernte gleichermaßen. Die Hierarchie der Materialien zeigt die übliche der Lernreihenfolge auf:
1.1. Brüche erkennen lernen

Bruchkegel
Für kleine Kinder und Einsteiger im Bruchrechnen geht es zuerst darum, überhaupt zu verstehen was ein Bruch ist und wie dieser entsteht. Das zeigen sehr schön die hölzernen Bruchkegel. Durch Auseinandernehmen der Kegel – also dem Teilen eines Ganzen – entstehen Brüche. Fügt man die Teile wieder zusammen, so ergeben sie wieder ein Ganzes. Ist dieses einfache Prinzip verstanden, steht die Grundlage allen Bruchrechnens.
1.2. Brüche addieren und subtrahieren
Mit den metallenen Bruchkreisen erweitert sich der Zahlenraum der Brüche auf bis zu 10/10. Hier kommen bereits erste Bruchrechnungen, das Ergänzen und Kürzen von Brüchen mit ins Lernprogramm. Z.B. wie viel ist 2/4 + 4+8 oder was 1 Ganzes – 6/10, usw.
1.3. Bruchrechnen üben
Wichtig ist natürlich, dass das Bruchrechnen regelmäßig geübt wird, bis es „wie im Schlaf“ funktioniert. Dabei arbeitet das Kind an Aufgaben wie: Erweitere den Bruch, Kürze den Bruch, Erkenne Brüche aus Flächen, Arbeite mit unechten Brüchen, …
1.4. Brüche zu Grad, Winkel und Prozent umrechnen

Brüche undprozent
Manchmal erscheinen Brüche selbst Erwachsenen als Herausforderung. Wird man allerdings mit Prozentrechnen, Gradeinteilung des Kreises und Rechnen mit Winkeln konfrontiert, ist schnell klar, wofür Bruchrechnen die Grundlage bildet. Am umfassensten arbeitet man an der mathematischen Thematik mit einer Kombination aus Gradmesser und metallenen Bruchkreisen. Alternativ bieten auch hölzerne Bruchkreise und Material zu Kreissegmenten eine klasse Möglichkeit, sich mit dem Umrechnen von Brüchen zu beschäftigen.
1.5. Dezimalbrüche verstehen lernen

Dezimalbrüche
Dezimalbrüche sind Kommazahlen, die uns allen geläufig sind. Natürlich weiß auch jeder Erwachsene, dass ½ = 0,5 und ¼ = 0,25 ist. Kinder müssen das erst lernen. Leicht zu vergleichen sind die Unterschiedlichen Darstellungsformen mit den Rechenstäben zu Brüchen, Prozent und Dezimalbrüchen. Vertiefend an Dezimalbrüchen gearbeitet wird dann mit dem Dezimalbruchkasten.
2. Den richtigen Einsprungpunkt in der Montessori-Bruchrechen-Hierarchie finden
Grundsätzlich fängt man mit dem Material an, das für das Kind den nächsten Lernschritt in der Reihenfolge darstellt. Ein Schüler in der Sekundarstufe wird den Lerninhalt der Bruchkegel bereits können und sich damit nur langweilen. Das ist natürlich dem Lernziel nicht dienlich. Wichtig ist es, genau einen Lernschritt nach „kann ich perfekt“ anzufangen. Alle vorhergehenden Übungen müssen sicher beherrscht werden – erst dann ist der Sprung in die nächste Lernebene notwendig und sinnvoll.